1. 시계열 데이터
: 시간의 흐름에 따라 관찰된 데이터이터: 시간의 흐름에 따라 관찰된 데이터
ex) 기온데이터, 주가데이터 등
대부분의 시계열 데이터는 비정상성 데이터이다. 시계열 데이터로 미래를 예측하기 위해서는 비정상성 데이터를 정상성 데이터로 변화하여 분석 모형을 설계할 수 있다.
시점에 따라 평균과 분산이 일정하지 않으면 데이터에 대한 신뢰도가 떨어지기 때문에, 평균과 분산이 일정하도록 전처리가 필요하다. (시계열 데이터를 정상성 데이터로 만들어야한다.)
> 구성요소
1) 추세(Trend)
- 데이터의 장기적인 증가 또는 감소 경향을 나타냄
- 시간에 따라 데이터가 지속적으로 오르거나 내리는 경향 등
2) 계절성(Seasonality)
- 일정 주기를 가지고 반복되는 패턴
ex) 월별 판매량, 계절별 온도변화
3) 순환성(Cyclic)
- 계절성보다 더 긴 주기를 가지는 비주기적 변동
4) 잔차(Noise, Residual)
- 위 요소들로 설명되지 않는 불규칙한 변동
- 데이터에 내재된 랜덤한 변동
2. 정상성
평균과 분산이 일정할 때 공분산도 단지 시차에만 의존하고 실제 특정 시점 t, s 에는 의존하지 않는 것이다.
즉, 시계열 데이터가 시점에 따라 평균이나 분산이 변하지 않는 것을 의미한다.
1) 차분(Difference)
: 현시점에서 전 시점의 자료를 빼는 것
- 평균이 일정하지 않은 시계열일 때 차분을 통해 정상화 할 수 있다.
- 일반차분(Regular difference): 바로 전 시점의 자료를 빼는 방법
- 계절차분(Seasonal difference): 여러 시점 전의 자룔르 빼는 방법으로 주로 계절성을 갖는 자료를 정상화 하는데 사용
2) 변환(Transformation)
- 분산이 일정하지 않은 시계열일 때 변환을 통해 정상화 할 수 있다.
정상시계열의 특징
* 어떤 시점에서 평균과 분산 그리고 특정한 시차의 길이를 갖는 자기공분산을 측정하더라도 동일한 값을 갖는다.
* 항상 그 평균값으로 회귀하려는 경향이 있으며, 그 평균값 주변에서의 변동은 대체로 일정한 폭을 갖는다.
* 정상 시계열이 아닌 경우 특정 기간의 시계열 데이터로부터 얻은 정보를 다른 시기로 일반화할 수 없다.
3. 시계열분석
- 수학적 이론모형: 회귀분석(계량경제)방법, Box-Jenkins(ARMA) 방법
- 직관적 방법: 지수평활법, 시계열 분해법으로 시간에 따른 변동이 느린 데이터 분석에 활용
- 장기예측: 회귀분석방법활용
- 단기예측: Box-Jenkins 방법, 지수평활법, 시계열분해법 활용
1) 이동평균법
- 일정기간별 이동평균을 계산하고, 이들의 추세를 파악하여 다음 기간을 예측하는 방법
- 시계열데이터에서 계절변동과 불규칙변동을 제거하여 추세변동과 순환변동만 가진 시계열로 반환하는 방법으로도 사용됨
- 간단하고 쉽게 미래를 예측할 수 있으며 자료의 수가 많고 안정된 패턴을 보이는 경우 예측품질이 높음
- 특정 기간 안에 속하는 시계열에 대해서는 둥일한 가중치를 부여함
- 시계열데이터에 뚜렷한 추세가 있거나 불규칙 변동이 심하지 않은 경우에는 짧은 기간의 평균을 사용하고 반대로 불규칙변동이 심한 경우 긴 기간의 평균을 사용함.
- 이동평균법에서 가장 중요한 것은 적절한 기간을 사용해야 함.
ex) 주가 추세 파악, 물품 수요 변화 탐지, 온도 변화 추세 분석, 센서 데이터 이상 탐지
2) 지수평활법

- 일정기간의 평균을 이용하는 이동평균법과 달리 모든 시계열 데이터를 사용하여 평균을 구하고 시간의 흐름에 따라 최근 시계열에 더 많은 가중치를 부여하여 미래를 예측하는 방법
- 단기간에 발생하는 불규칙 변동을 평활하는 방법
- 자료의 수가 많고 안정된 패턴을 보이는 경우일수록 예측 품질이 높음
- 지수평활법에서 가중치의 역할을 하는 것은 지수평활계수이며 불규칙변동이 큰 시계열의 경우 지수평활계수는 작은 값은, 불규칙변동이 작은 시계열의 경우 큰 값의 지수평활계수를 적용
- 지수평활계수는 예측오차를 비교하여 예측오차가 가장 작은 값을 선택하는 것이 바람직
* 예측오차: 실제 관측치와 예측치 사이의 잔차제곱합
- 지수평활계수는 과거로 갈수록 지속적으로 감소
- 지수평활법은 불규칙변동의 영향을 제거하는 효과가 있으며 중기 예측 이상에 주로 사용
- 단순지수 평활법의 경우 장기추세나 계절변동이 포함된 시계열의 예측에는 적합하지 않음
3) 자기회귀모형(AR 모형, Autoregressive model)


- 자기 자신의 과거 값이 미래를 결정하는 모델
- 부분자기상관함수(PACF)를 활용하여 AR(p)모델 선정
- AR모형은 정상성과 오차항의 독립성을 가져야 함

- PACF가 p시점 이후 급격히 감소하면 AR모형이 적합 (ACF는 빠르게 감소)
4) 이동평균모형(MA 모형, Moving Average model)


- 백색잡음들의 선형결합으로 표현되는 모델
* 백색잡음: 시계열 모형의 오차항으로 서로 독립적이며 동일한 분포를 따름. 발생원인을 알려져 있지 않음.
- 자기상관함수(ACF)를 활용하여 MA(q)모델 선정
- 유한한 개수의 백색잡음의 결합이므로 언제나 정상성을 만족
- 단기적 변동만 모델링하므로 장기적 추세반영 어려움
- 실제 데이터에서 오차항이 항상 독립적이지 않을 수 있음

- ACF가 q시점 이후 급격히 감소하면 MA모형이 적합 (PACF는 빠르게 감소)
5) 자기회귀누적이동평균 모형(ARIMA, Autoregressive integrated moving average model)
Chapter 8 ARIMA 모델 | Forecasting: Principles and Practice
2nd edition
otexts.com
- 비정상시계열모형
- 차분이나 변환을 통해 AR모형이나 MA모형, 이둘을 합친 ARMA모형으로 정상화가능
- ARIMA(p,d,q)에서 p는 AR모형, q는 MA모형과 관련이 있는 차수
- d=0이면 ARMA(p,q)모형이라 부르고, 이 모형은 정상성을 만족
ARMA(0,0)일 경우 정상화 불필요 - p=0이면 IMA(d,q)모형이라 부르고, d번 차분하면 MA(q)모형을 따름
- q=0이면 ARI(p,d)모형이라 부르고, d번 차분하면 AR(p)모형을 따름
ex) ARIMA(1,1,2)의 경우 1 차분 후 AR(1), MA(2), ARMA(1,2)선택 활용하는데, 가장 간단한 모형을 택하거나 AIC를 적용하여 점수가 가장 낮은 모형 선정
6) 분해시계열
- 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
- 회귀분석방법을 주로 사용
> 분해방법
- Additive Model: 모든 요소가 더해지는 형태로 데이터 변동 폭이 일정할 때 적합
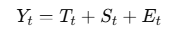
- Multiplicative Model: 각 요소가 곱해지는 형태로 데이터 변동폭이 시간에 따라 달라질 때 적합

> 분해과정
- Trend Estimation: 이동평균법이나 회귀분석을 사용하여 데이터의 장기적인 추세 추정
- Seasonal Decomposition: 추세 제거후 계절 패턴 계산
- Residual Calculation: 원 데이터에서 추세와 계절성을 제거하고 잔차 계산(모델링이 충분한지 확인하고 추가적인 요인탐색)
'통계학 > 통계' 카테고리의 다른 글
| [통계분석] ANOVA (분산분석) (1) | 2024.12.23 |
|---|---|
| [통계분석] t-test (t-검정) (2) | 2024.12.22 |
| 상관분석 정의 및 종류 + 예시(w. Python) (3) | 2024.12.09 |
| 정규성 검정 종류 및 Python Code (1) | 2024.12.07 |
| [확률분포] 연속형 확률분포 (2) | 2024.12.01 |

